MACHINE LEARNING WITH ORANGE

In my last blog we looked at coding basics and the differences between CLI and GUI programs, but now we'll have a look into the wonderful world of Machine Learning (ML). In this blog we're going to break down models and create some ML model using the GUI program 'Orange'.

To put it simply, Machine Learning is a process of using data to create a model, which then predicts or decides on an outcome for future data. For example, if you watch a bunch of Game of Thrones fan theories on YouTube, your search history (input data) is fed into a model (created by YouTube) which then decides or predicts what your next video should be (output data). This is called Machine Learning because the machine makes the decision/prediction without being explicitly programmed to (ie no one is sitting on the other side of your computer and recommending what to watch in real time).

Firstly a couple of mathematical definitions.

Formula/Equation

A mathematical relationship or rule expressed in symbols.

Algorithm

Technical Version - A precise step-by-step plan for a computational procedure that possibly begins with an input value and yields an output value in a finite number of steps.

Tuna Version - a recipe or set of steps to turn input data into a desired output data, usually containing mathematical formulas or equations.

Model

Technical Version– a physical, conceptual, or mathematical representation of a real phenomenon that is difficult to observe directly.

Tuna Version - a case specific representation of data, in most cases built by an algorithm.

WHAT IS A MODEL BEER EXAMPLE

We'll start with something simple and define what a model is using an example. Let's say I had a bunch of people around for a Tupperware party on the weekend which went from 11:00am to 8:00pm (9 hours) on Sunday afternoon. Before the party I quickly drove down to the bottle shop to buy a (warm) box of Coopers Pale Ale, and as soon as I got home (11:00am) I cracked my first beer then put the rest in the fridge. I decided (as I disgustingly sipped a warm beer) that I would only have one beer every hour to prevent myself getting too drunk and so I could make sure the party ran smoothly. My bar fridge isn’t operating as well as it used to these days, and I know people would be opening and closing it all day, so every time I had another beer I decided I would measure the temperature of it (°C) to assess how well my fridge was working. The data (results) of the temperature of beer at each hour is below. Logically, we would expect the temperature to drop over time and looking at the data we can see that it does.

The next weekend I decide to host the same party with the same beer in the exact same environment. At 2:30pm (3.5hrs after 11:00am) Brad rocks up to the party and asks 'Hey mate have you got any cold beer? if so what is the exact temperature of said beer in degrees celsius?'. I don't know off the top of my head, but I know from last week that after 3 hours in the fridge the beer is 15.6 degrees and after 4 hours the beer is 11.2 degrees. Logically you would think that the temperature is somewhere between 11.2 - 15.6 degrees but what if I wanted a more mathematically exact number. This is where I can use my data from last week to create a model.

To create a model I have to choose an algorithm (my mathematical recipe of steps) that I think best suits the data . I have two variables in the data, hours and temperature, so I'm going to try a simple linear regression algorithm (a line of best fit). In this case I just plugged the data into excel and used their linear regression algorithm, which uses a least squares method (I made the line of best fit in a scatter graph). A visualisation of the data and model can be seen in the image below. Remembering from school, the equation of a line is in the from of y=mx+c (where m=slope and c=intercept), which is the mathematical basis of our model. Using the linear regression algorithm, excel has stated that our 'case specific' model is y=-2.56x+23, where y is the temperature and x is how many hours the beers have been in the fridge.

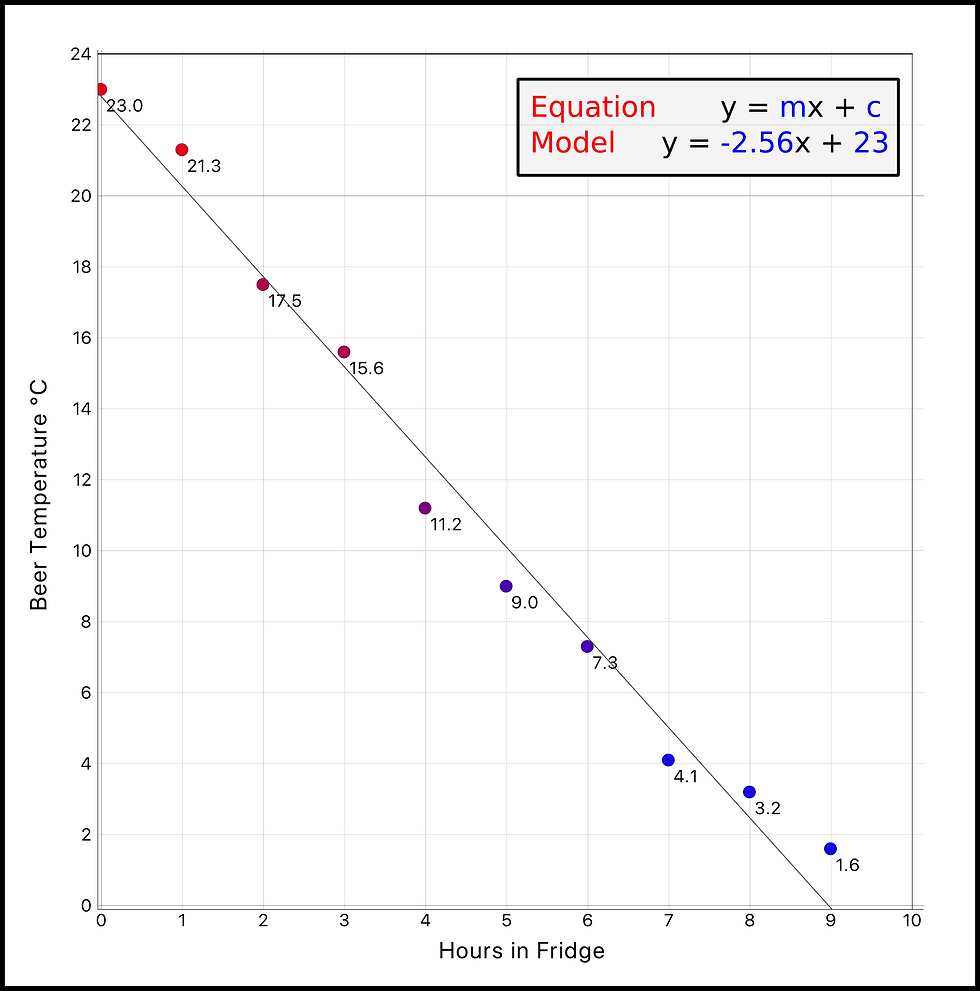
So at 2:30pm Brad asks me again slightly louder 'Hey mate have you got any cold beer? if so what is the exact temperature of said beer in degrees celsius?'. I can now enter the input data of 3.5hrs into the model and return a temperature.

y = -2.56(x)+23

Temperature = -2.56(Hours)+23

Temperature = -2.56(3.5)+23

Temperature = 14.0 degrees C

At 2:30pm the model says that the temperature of beer will be 14.0 degrees celsius which seems to fit our data set pretty well. Visually this model looks good and so far seems mathematically sound so it must be good right? WRONG. According to this model, if I leave beer in my fridge for 4 days (96 hours) it would be -222.8 degrees C. I don't think my fridge can do that, especially if it's set at 4 degrees. It is absolutely crucial to know the nature and environment of the data you are trying to model and constantly question whether it makes sense in real life.

So in this case I could say that the model works up until approximately 9 hours into a party and after that it's garbage, but maybe I can make it better. I could keep collecting temperature data after 9 hours, I could try using an exponential regression algorithm, or I could even collect different variable data that might affect the temperature (total time that the fridge door was open during each hour or total surface area of other items in the fridge at each hour).

What we have achieved here is a very simple machine learning model that predicts the temperature of beer from the amount of hours it has been in the refrigerator. To create more complex ML models from data with more variables and less obvious relationships there is a great GUI program called 'Orange' which we will have a look at.

GEOLOGY EXAMPLE

Let's do a geochemistry example. In 1979 a few blokes wrote a book called 'The Interpretation of Igneous Rocks' which included the, now very well known, Total-Alkali-Silica (TAS) classification diagram. This diagram classifies igneous rocks into their individual lithologies based on their Alkali (Na2O+K2O) content and their SiO2 content. The classification boundaries were decided upon by the International Union of Geological Sciences, Subcommission on the Systematics of Igneous Rocks who drew the linear boundaries around clusters of known rock types.

In this model, you input your SiO2 and total alkali values and then you get your lithology as an output. What if we had a whole lot more geochemistry data? Could we create a similar classification model using Machine Learning algorithms?

Using the GEOROC open source geochemistry database, I created a dataset containing the chemistry of 100 different Granites (Felsic), Diorites (Intermediates), Gabbros (Mafic) and Harzburgites (Ultramafic). We will use this dataset to create a Machine Learning model that classifies plutonic rocks into one of these 4 lithologies based upon their chemical composition. Firstly we need to look at some of the Machine Learning Nomenclature.

FEATURES - Features is the name for variables in the machine learning world. They can be split into 4 data types; numeric, categorical, text or time series. Features are the columns in a data table.

INSTANCES - The instances are the rows in a data table. They are data points which have associated feature values.

TARGET VARIABLE - Our dependent feature (or variable) that we are trying to classify/predict.

In our data set we have our Target Variable which is 'Rock' (keepin' it simple here), we have 94 Features (all the elements and/or oxides) and we have 400 Instances (100 each of Granite, Diorite, Gabbro and Harzburgite). We now have a clean dataset and everything is ready to go into Orange.

Before diving straight into creating a model it is important to know what kind of algorithms we should use. There are 3 different learning styles; Supervised, Unsupervised and Reinforcement Learning.

Supervised Learning - In supervised learning we use labelled features and target variables to create the model. In this example we know the Rock types and we know what each individual featues (columns) are because they are labelled (Cu, Au, SiO2 etc). Supervised learning can further be split into Regression (using continuous/numeric values like the beer example) or Classification (using categories like this geochemistry example).

Unsupervised Learning - This uses data that has not been labelled in hope to 'group' instances that have similarities between the features. Algorithms can either be split into the categories of Clustering or Association. An example would be receiving the above data sheet without our element names and rock types, and then trying to decipher how many different rock types there are, effectively 'going in blind'.

Reinforcement (or Semi-Supervised) Learning - I don't really know much about this and I feel it doesn't have many applications in geosciences, however for those interested this might be worth a look.

ORANGE DATA MINING

Orange is a very visually pleasing open-source program that allows data analysis and visualisation for all experience levels from chump to Chuck Norris. It uses a 'drag and drop' widget system to create work flows to take your raw input data to wherever your heart desires. For the sake of this blog I won't go too deep into Orange's capabilities but instead I will show you a workflow for producing a machine learning algorithm.

So just to clarify, we are going to use the geochemistry of 400 different known rock types to create a model that will classify samples into either Granite, Diorite, Gabbro or Harzburgite based upon their chemical composition.

This is what an Orange workflow looks like, with each widget serving its individual purpose. On the left hand side you can see a panel containing all the widgets that you can drop and drag them onto the workflow canvas. The links seen between all the widgets are to connect them and to have the data 'flow' through the workspace. We'll look at each widget individually.

1. File

This is where we load our data table into orange and define what data type our features are. In this case we are loading an Excel table file (.xlsx) with our 94 (95 if we include the target variable 'ROCK') features. As mentioned previously, the data in our features can come in the form of numeric, categorical, text or time series. To access the widget double click on it, navigate to and open the file then define what each feature's (column) data type is. In this case ROCK will be categorical and the remainder will be numeric. Under the 'Role' column ROCK also needs to be put as our target variable as it's what we are trying to classify.

2. Rank

Rank assesses the relationship between the features and target variable and tells us how well they correlate. As geologists we know that the biggest differentiating features between mafic and felsic rocks are the magnesium and silica content. Rank is telling us that MgO varies the most between the 4 lithologies, followed by SiO2, Al2O3 etc etc. Here we can decide what features can go into our model. There is a goldilocks zone of how many features should be included into to make an optimum model and it is determined on a case by case basis. You don't want too few and you don't want too many, thankfully in Orange it is easy to just select how many pass through the workflow by just highlighting them. In this case I've selected the top 10 features shown below.

There are several different scoring methods as seen in the left side panel. The Orange website has more information on how each of these are determined.

3. The Juicy Bits

These 5 pink widgets are Machine Learning algorithms, each with their own way of mathematically classifying/predicting our target variable using the geochem data. In the beer example we used a a single regression algorithm to create our model, in Orange we can use many different algorithms at once and compare them. There is an ever-growing list of ML algorithms but in this workflow I have used k-Nearest-Neighbour (kNN), Support Vector Machines (SVM), Naive Bayes, Random Forest and Adaptive Boosting (AdaBoost). Each algorithm has parameters that can be tweaked in attempt to increase model accuracy.

Machine Learning algorithms can be quite (definitely are) mathematically intense and difficult to break down into simple terms. There are many documents online that outline each specific algorithms function, but the Orange documentation is usually pretty good. This is a good summary for selecting the right algorithm too.

4. Test and Score

When you create a Machine Learning model you need a way to make sure your model actually works. We can do this by randomly splitting the data set into 'training' and 'test' data. The training data is used to create the model and the test data is used to determine the accuracy of the model. The 5 different models created by the training data ignores the target variable in our test data (just looks at the chemistry and not the rock type) and attempts to classify/predict what rock type each instance would be. The predicted rock type is then compared to the actual known value in our test data and each model is scored based on accuracy. In this case the split is selected at 80% training and 20% test, representing 320 and 80 instances respectively.

To put it simply we, the operator, know what the target variables are for both our training and our test data, but our model only knows the training data. eg the model knows that the training data is Homer Simpson and now has to predict whether the test data is or not.

When splitting our training/test data we can choose how many times we wish to repeat the split of data. If we choose to repeat the sampling 10 times, we will end up with 10 different sets of 320/80 (training/test) splits from the data. Repeating the random splitting increases the accuracy of our model.

The Test and Score widget compares each models target variable results to the actual data and tells us how good the model is. The performance of a model is represented by the Area Under Receiver-Operator Curve (AUC), Classification Accuracy (CA), F1, Precision and Recall. For the sake of simplicity, we will only look at the classification accuracy of our model which is the portion of correctly classified target variables. From the list we can see that the accuracy of kNN is 85.6%, SVM is 93.9%, Random Forest is 93.8%, Naive Bayes is 85.6% and AdaBoost is 90.1%. Looking at this we can see the SVM and Random Forest algorithms create the most accurate machine learning models in this example.

Here we have created 5 models, and if we gave each model a brand new set of 400 sample assay results we would expect that SVM or Random Forest to be the most accurate in telling us what the rock types were, and kNN or Naive Bayes to be the least accurate.

5. Confusion Matrix

The Confusion Matrix tells us where our models strengths and weaknesses lie in regards to their classification. Below is an example of the SVM algorithm confusion matrix. It shows us what the actual values of our target variables are and what the model predicted them as. Of the 200 Diorite test data samples (20 samples multiplied by the 10 repeat splits) SVM has classified 183 as Diorite, 15 as Gabbro, 2 as Granite and 0 as Harzburgite. Looking at the remainder of the matrix it is noticeable that our model has some trouble differentiating between Diorite's and Gabbro's, but has almost no issues classifying Harzburgite from the geochemical data. Geologically this makes sense as Diorites and Gabbros have a similar chemistry.

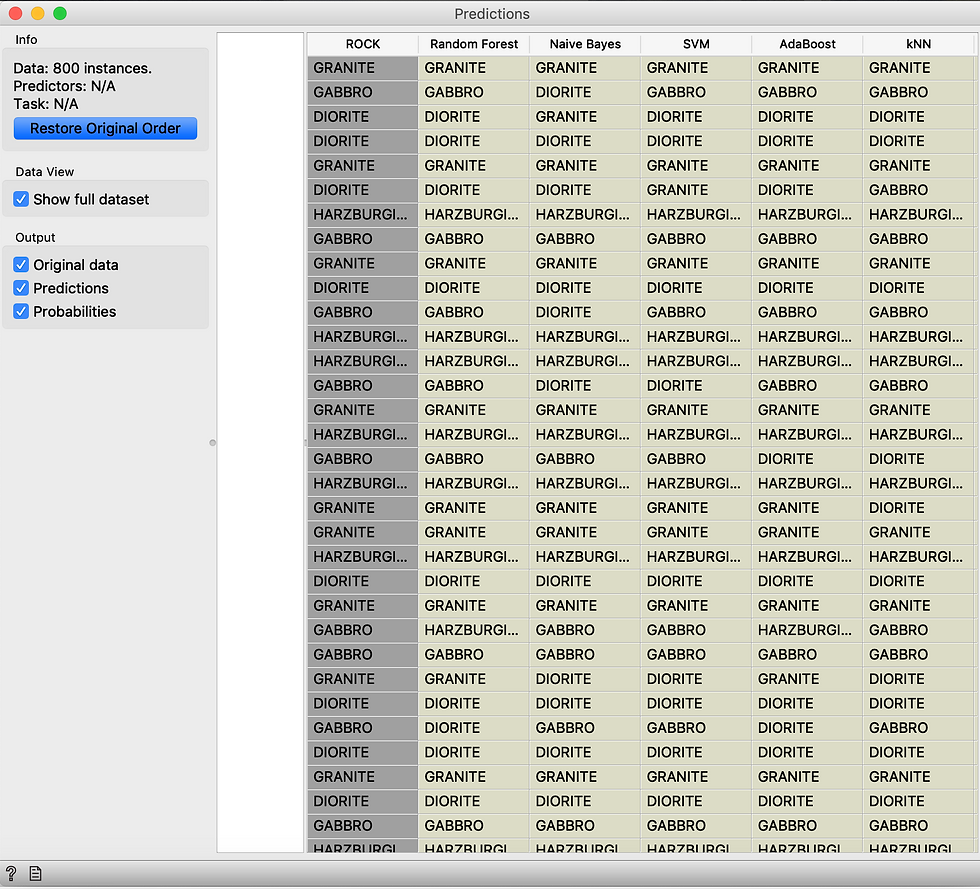
6. Predictions

Predictions is another way of visualising how well the model has classified out target variable. In this widget a table of each individual instance is shown and what each model has classified it as. Using both Predictions and the Confusion Matrix we can see where we can improve out model. For example it looks like we need a better way to seperate our Diorite and Gabbro classification.

Let's say we are happy with our Random Forest model and we have decided that we want to use that as our classifier. Orange has a 'Save Model' function, where you can save the model as a pickled model (pkcls) file. This file type can be used both in Orange (using the load model widget in a new workflow) or in Python, where new assay data can be tested and then the model classify samples into the four rock types.

Here comes Brad again with his 14.0 C Pale Ale and a USB flash drive. 'Hey mate I've got a bunch of geochemical data for Granites, Diorites, Gabbros and Harzburgite's and I'm having trouble telling them apart from the data, can you help?'. Now that we have our model, we can send Brad's data into our Random Forest model and tell him with 93.8% accuracy which rock type each sample is.

However, why even create a model like this when you can obviously just pick up the rock sample and look at its mineralogy? Even if you can't tell straight away wouldn't you look at the assays and be able to pick it out pretty quick? (even though mineral estimates are highly variable and subjective from geo to geo).

What if things weren't so straightforward. Let's say we find ourselves in a base metal enriched geological province, and we had several different intrusive events but only one of these events is associated with mineralisation. All different intrusions have almost the exact same mineralogy with slightly varying chemistry but not easily noticed by the human eye. You could plug all the data you have into a Machine Learning algorithm and create a model that classifies the intrusions based upon patterns a human eye might not be able to recognise.

As mentioned above in our beer example, it is extremely important to understand the nature of our problem or task we are trying to achieve through machine learning. Just because we can throw a bunch of data into an algorithm and create a good model doesn't mean we should. Understanding the geology and science should be your first point of call. Having said that I hope this write up has at least given a starting point for creating models and the plethora of possibilities that Orange can provide.